最新記事公開時にプッシュ通知します
スーパーマリオシリーズで「クリア不可能なコース」が作成できることを数学的に証明 米MITの研究者ら【研究紹介】
2024年5月24日


先端テクノロジーの研究を論文ベースで記事にするWebメディア「Seamless/シームレス」を運営。最新の研究情報をX(@shiropen2)にて更新中。
米マサチューセッツ工科大学(MIT)に所属する研究者らが発表した論文「You Can’t Solve These Super Mario Bros. Levels: Undecidable Mario Games」は、任天堂のスーパーマリオシリーズの一部のゲームにおいて、プレイヤーがクリアすることが理論上不可能なコースを数学的に証明した研究報告である。
研究内容
対象となったゲームは、「New スーパーマリオブラザーズ」シリーズ(オリジナル版、Wii、U、2)と、「スーパーマリオメーカー」1および2の全ゲームスタイル(スーパーマリオブラザーズ1、3、ワールド、New スーパーマリオブラザーズU、3Dワールド)である。
研究チームは、これらのゲームにおいて、ステージがクリアできるかどうかの判定が決定不可能であるとの証明を試みた。この証明は、各場所に配置できる敵キャラクターの数や、画面上に同時に存在できる敵の数に制限がないこと、さらに、制限時間が非常に長いか無限であることを前提とする。
証明には、研究チームが開発した「カウンターガジェット」(Counter Gadgets)という理論的枠組みを用いた。これは、各場所に存在する敵の数でカウンターの値を表現し、敵の出現と消滅によって、値の増加・減少、そして0かどうかの判定を行うことで、コンピュータープログラムと同等の複雑な動作をゲーム内で実現するものである。

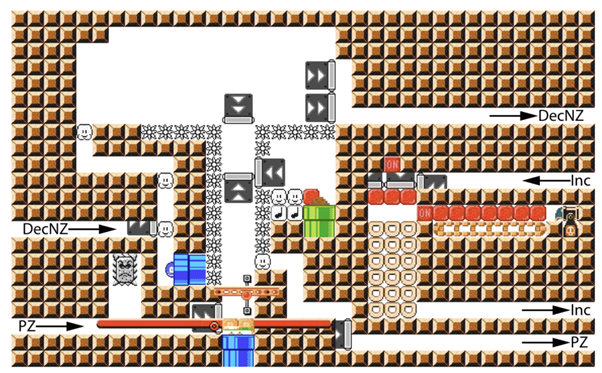
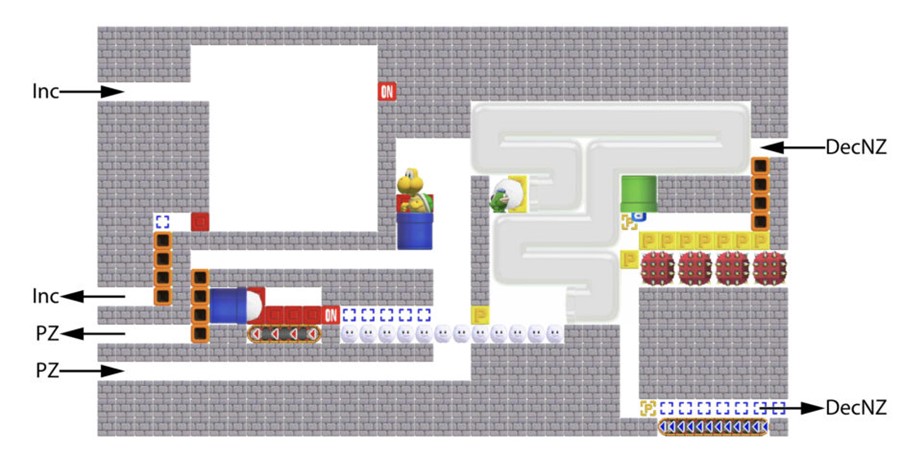
このカウンターガジェットを用いて、スーパーマリオシリーズが決定不可能であることを証明する方法は以下の通りである。まず、カウンターガジェットを使ってゲーム内にカウンターマシンを構築する。このカウンターマシンは、カウンターの値を1増やす操作(例えば、特定のブロックを叩いてクリボーが生成される)、カウンターの値がゼロでない場合に1減らす操作(例えば、クリボーを踏んで倒す)、カウンターの値がゼロなら特定の命令に進む操作、という3つの操作を持つ単純なコンピューターである。
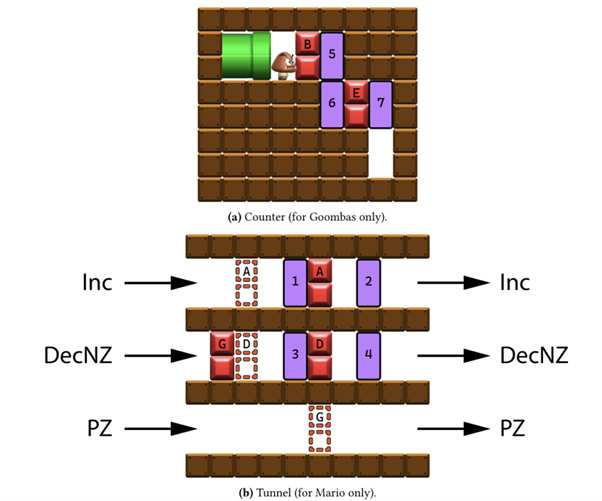
次に、このカウンターマシンの動作を使って、エージェント(マリオ)が特定の場所に到達できるかどうかを確認する。そして、このカウンターマシンを使った問題が「停止問題」と同じくらい難しいことを示す。停止問題とは、あるプログラムが特定の入力で停止するかどうかを決定する問題であり、ここではプログラムが無限ループに入るか、最終的に停止するかを判断する問題である。これは数学的に証明されており、どんなアルゴリズムを使っても一般的には解けない決定不可能な問題である。
そして、ゲーム内でカウンターマシンをシミュレートできるならば、カウンターマシンが停止するかどうか、という停止問題をゲーム内の問題として表現できる。具体的には、カウンターマシンが特定の状態に到達するかどうかを判断する問題をつくることができる。これにより、ゲーム内の問題が停止問題と同じレベルの複雑さを持つことを示し、結果としてこの問題が決定不可能であることを証明する。

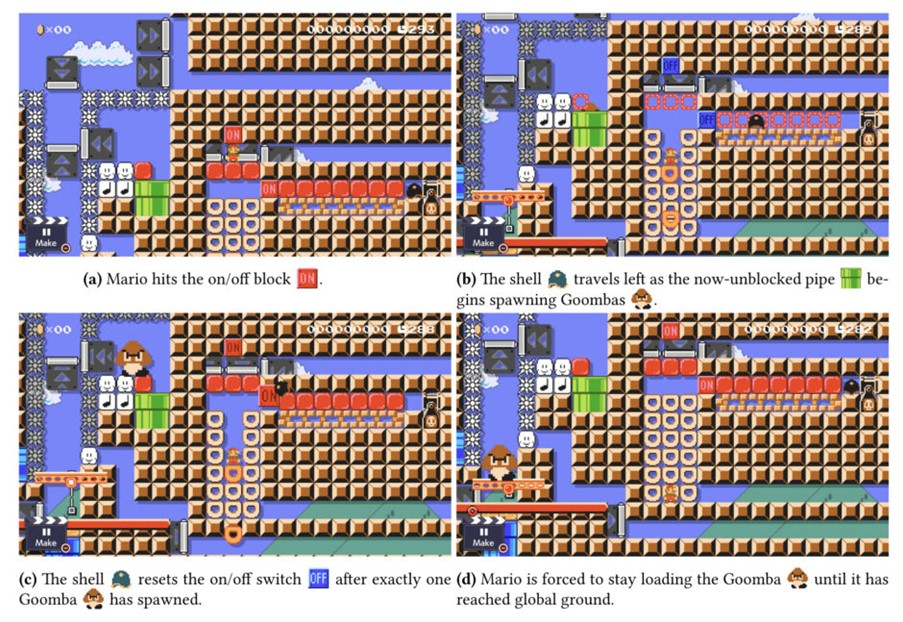

研究結果
実験結果は次の通りである。まず、「New スーパーマリオブラザーズ」シリーズにおいて、単一画面内に普遍的なカウンターマシンを構築することができると示された。これには、マリオの位置によってブロックの存在を切り替える強力な「イベント」メカニクスが利用された。このイベントを活用することで、特定の場所に到達するためのカウンターマシンを設計し、単一画面のレベルでも決定不可能であることが証明された。
また、「スーパーマリオメーカー」シリーズの全てのゲームスタイルにおいても、普遍的なカウンターマシンを構築できると示された。これにより、これらのゲームも決定不可能性があることが証明された。これらのゲームスタイルでは、ゲームエンジンが画面外のオブジェクトを記憶する特性が利用された。
Source and Image Credits: MIT Hardness Group, Hayashi Ani, Erik D. Demaine, Holden Hall, Ricardo Ruiz, Naveen Venkat. You Can’t Solve These Super Mario Bros. Levels: Undecidable Mario Games.
関連記事

画像1枚から操作可能なゲームを生成できるAIモデル「Genie」 Google DeepMindなど開発【研究紹介】

【ABA Games】インディーゲーム制作歴40年。PC黎明期から生成AI時代まで折れずに続ける理由

趣味でつくった2Dゲームエンジンが導いた「幸」あるキャリア。己の欲求に従い続けてきた「Ebitengine」開発者に迫る
人気記事