球を分解→元と同サイズの球を2個作れてしまう「バナッハ=タルスキーのパラドックス」、p進数の世界でも成立と発表【研究紹介】

ポーランドのジェシュフ大学に所属するKamil Orzechowski氏が発表したプレプリント論文「The Banach-Tarski paradox in complete discretely valued fields」は、p進数体をはじめとする完備離散付値体という、通常の実数とはまったく異なる距離構造を持つ数の世界でも、「バナッハ＝タルスキーのパラドックス」が成り立つことを証明したとする研究報告だ。

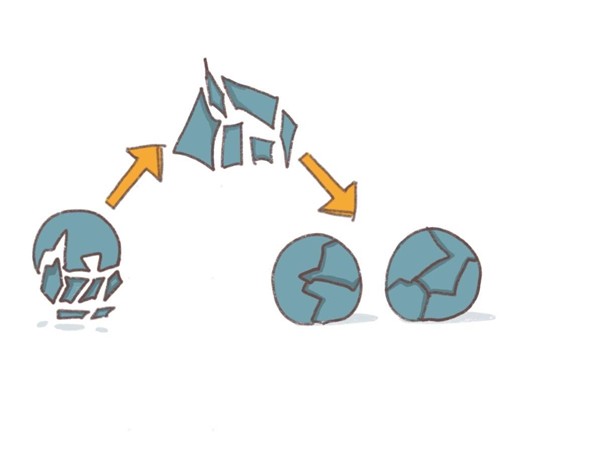
• keyboard_arrow_down バナッハ＝タルスキーのパラドックスと「完備離散付値体」について
• keyboard_arrow_down 無限の桁を「偶数・奇数」に分けて「2次元」へ

バナッハ＝タルスキーのパラドックスとは、ひとつの球を有限個のピースに切り分けて、回転や平行移動だけで組み替えると、もとと同じ大きさの球が2個できてしまうという定理。体積が2倍に増えるかのように見えるためパラドックスと呼ばれている。

実際には体積が増えるのではなく、切り分けたピースが複雑すぎる形をしていて、そもそも体積という概念を適用できないというのがからくりだ。ただしこの現象は3次元以上のユークリッド空間でしか起こらず、平面や直線の上では成立しないことが知られている。

今回の研究は、このパラドックスの分解に通常の実数とはまったく異なる距離の感覚を持つ完備離散付値体（特にp進数）を適用するという試み。通常の数の世界では1と1.001は近いが、p進数の世界では2つの数の差が素数pで何回割り切れるかによって距離が決まり、多く割り切れるほど近いとみなされる。

例えば、2進付値の意味では、0と8の距離（8 = 2³なので、差の8は2で3回割れる）と、0と1の距離（差の1は2で一度も割れない）を比べると、8のほうが1よりも0に近い。この奇妙な距離（超距離）のもとでは、球の内部のどの点を中心と呼んでも構わないのだとか、三角形がすべて二等辺になるといった、ユークリッド幾何とはかけ離れた不思議な性質が成り立つ。

Orzechowski氏の以前の研究では、p進数体上に作った2次元以上の空間で、アフィン等長変換（回転や平行移動のように、距離を変えない変換）の群に関してバナッハ＝タルスキーのパラドックスな分解が可能であることを示していた。しかし1次元、つまりp進数体そのものについては、この手法は通用しなかった。1次元のアフィン等長変換群は従順群であり、従順群のもとではパラドックスな分解が原理的に不可能だからだ。

そこで今回の研究では、アフィン等長変換群よりもはるかに大きい等長変換群全体に着目した。p進数体の等長変換群は、アフィン等長変換群よりずっと豊かな構造を持つことが知られている。

ポイントとなったのは、p進数の無限に続く桁を偶数番目と奇数番目に振り分けるというアプローチで、この操作により、1個のp進数が2個のp進数の組に変換され、1次元の問題が2次元の問題に変換できる。2次元ではすでにパラドックスな分解が成功しているので、その結果を逆操作で1次元に戻す。このとき、2次元のアフィン変換が1次元の等長変換に変わることが示され、こうして1次元のp進数の世界でもパラドックスな分解が実現したという。

結論としては、p進数体そのもの、およびp進数体の中のすべての球と球面は、4個のピースに分割してパラドックスに組み替えができることが示された。また、ピースをベール性（数学的に扱いやすいピース）に分解した場合では、6個のピースで同じことが可能だとわかったとのことだ。さらに、局所コンパクトという性質を持つ体では、有界（ある範囲に収まっている）で内部を持つ（中身の詰まった）2つの集合（塊）がどんな形や大きさであっても、一方を有限個のピースにバラして組み立て直せば、もう一方にぴったり変えられることも示された。

Source and Image Credits: Orzechowski, K. (2026). The Banach-Tarski paradox in complete discretely valued fields.