最新記事公開時にプッシュ通知します
ゲイツ氏も研究した50年来の未解決問題“焦げたパンケーキ”ソートに新成果「奇数枚の場合は完全解決」【研究紹介】
2026年1月20日


先端テクノロジーの研究を論文ベースで記事にするWebメディア「Seamless/シームレス」を運営。最新の研究情報をX(@shiropen2)にて更新中。
スウェーデンのウメオ大学に所属する研究者らが発表した論文「Exact number of flips required to sort a burnt stack of pancakes」は、「焦げたパンケーキ」問題の奇数枚の場合を完全に解決したとする研究報告である。

「昇順」&焦げてない面が全て上を向いている状態へするまでの数
パンケーキソート問題は1975年にJ.E.グッドマン氏が提起し、1979年に米マイクロソフト創業者ビル・ゲイツ氏とクリストス・パパディミトリウ氏が正式に研究した古典的な組合せ最適化問題である。異なる大きさのパンケーキが積み重なった山を、フライ返しで上からk枚をひっくり返す操作だけで大きさ順に並べ替えるには何回の操作が必要か、という問いだ。
この問題には2つの変種がある。通常版と「焦げ」版である。焦げ版では各パンケーキの片面が焦げており、最終的に全てのパンケーキを大きさ順に並べるだけでなく、焦げた面を全て下に向けなければならない。ウェイターがコックから受け取った焦げたパンケーキの山を客に出せる状態にする、という状況を想像するとわかりやすい。
今回研究チームは、焦げたパンケーキ問題の特定のインスタンスについて新たな成果があったと報告した。扱ったのは、n枚のパンケーキが大きさ順に並んでいる(昇順)が全て焦げた面が上を向いている状態から、昇順かつ焦げてない面が全て上を向いている状態へ変換するのに必要な最小フリップ回数T(n)である。
1997年にHeydari氏とSudborough氏がnを4で割った余りが3(n ≡ 3 mod 4)の場合について上界を示し、2011年にCibulka氏がこれと一致する下界を証明して、この場合の正確な値が確定していた。しかしnを4で割った余りが1の場合については未解決のままだった。
今回研究者らはスーパーコンピュータを用いた探索により、nを4で割った余りが1(n ≡ 1 mod 4)かつn≧29の全ての場合について、T(n)が(3n+3)/2の整数部分に等しいことを証明したと報告している。この結果は、Cibulka氏が示した下界と一致しているという。
本研究で提案されたアルゴリズムが理論的な証明を与えたのはn≧29の範囲だが、それより小さな値については、過去の研究における計算機探索によりすでに最適解が確定している。よって、本研究で奇数nについてはT(n)の正確な値が完全に決定された、としている。
偶数nについては2つの候補値が残っているとし、今後の課題となっている。
Surce and Image Credits: Gerold Jäger, Nacim Oijid. Exact number of flips required to sort a burnt stack of pancakes.
関連記事

GoogleのAIが通説覆す巨大な「ハイパーキューブ」(超立方体)を発見、人間の数学者が証明と報告【研究紹介】
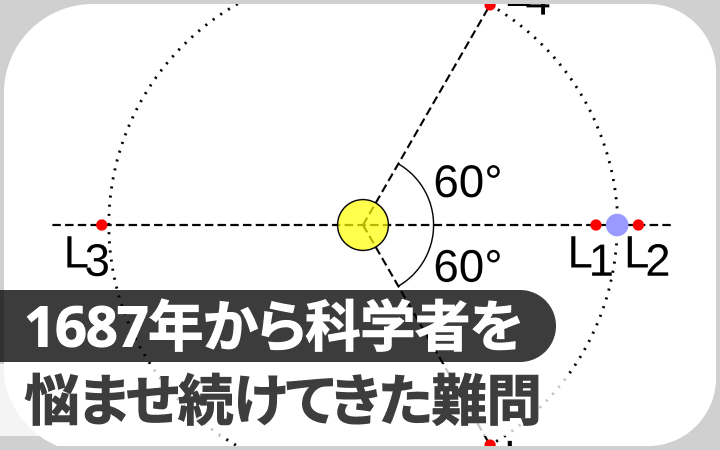
SF小説『三体』の元ネタ、300年来の“あの難問”に新展開。カオスの仕組みを数学者が解明と発表【研究紹介】

トランプを“適当に”混ぜてちゃんとランダムになるのは何回目? 必要なシャッフル回数分かる公式を発見か【研究紹介】
人気記事





