GoogleのAIが通説覆す巨大な「ハイパーキューブ」(超立方体）を発見、人間の数学者が証明と報告【研究紹介】

米国のウィスコンシン大学マディソン校やオーストラリアのシドニー大学などに所属する研究者らが発表した論文「Bruhat intervals that are large hypercubes」は、AIを用いた探索によって、「対称群」という構造の中に、従来予想されていたよりも遥かに巨大な秩序だった領域である「ハイパーキューブ」（超立方体）が存在することを発見した、という研究報告だ。

• keyboard_arrow_down まずは「対称群」についておさらい
• keyboard_arrow_down AIが「最適な構造をつくるプログラム」自体を進化させることで

この発見を理解するために、まずは「対称群（S_n）」という言葉を理解する。対称群とは、n個のものを並べ替える操作（置換）のパターンをすべて集めた数学的なグループのことである。 例えば、1、2、3と書かれた3枚のカードを一列に並べ替える状況を想像してみてほしい。このとき、並べ方は以下のようになる。

• ●「そのまま動かさない」（1, 2, 3）

• ●「2枚を交換する」（1, 3, 2 ／ 3, 2, 1 ／ 2, 1, 3）

• ●「全体をずらす」（2, 3, 1 ／ 3, 1, 2）

このように合計で6通りの並べ方が存在し、これを「3次の対称群（S_3）」と呼ぶ。

次に、この複雑な並べ替えの世界に秩序を与える「ブリュア順序」を理解する。 先ほどの3枚のカードを使って説明しよう。初期状態「1, 2, 3」から、隣同士を入れ替える操作を繰り返して、最終的に逆順の「3, 2, 1」を目指すと仮定する。このとき、「1, 2, 3」から出発して「3, 2, 1」にたどり着くまでの過程にある並べ方は「順序関係がある（つながっている）」とみなされる。

しかし、ゴールへのルートは一本道ではない。「1, 2, 3」から「2, 1, 3」を経由するルートもあれば、「1, 3, 2」を経由するルートもある。このとき、別々の分岐ルートにある「2, 1, 3」と「1, 3, 2」同士は、どちらが先とも後とも言えないため、「順序関係がない（比較できない）」とみなされる。

このルールに従って対称群全体を地図のように描くと、ある並べ方から別の並べ方への無数のルートが張り巡らされた、極めて複雑なネットワーク図が出来上がる。

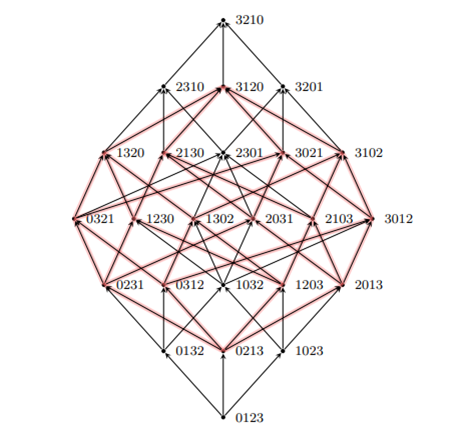
次に、「超立方体」を理解する。 超立方体とは、2次元の正方形や3次元の立方体を、より高次元（4次元以上）へと拡張した図形を指す。 この図形の最大の特徴は、その構造が「スイッチのONかOFFか（1か0か）」の組み合わせだけで説明できる点にある。例えば、スイッチが2つなら「オン・オン」「オン・オフ」などの4通りで四角形（2次元）になり、3つなら8通りで立方体（3次元）になる。スイッチが増えれば増えるほど、次元が高く巨大な図形になっていく。

本研究では、ブリュア順序を備えた対称群S_nの内部にどれほど大きな超立方体が現れるかという問題に向き合う。

従来、この超立方体の次元は、カードの枚数nが増えてもnに比例する程度だった。ブリュア順序の制約によって複雑に入り組んだネットワークの中に、シンプルで自由な超立方体が、それほど巨大に広がるはずがないと思われていたからである。

しかし、論文によると、Google DeepMindの進化型AI「AlphaEvolve」は、その常識を打ち破った。AIは特定の数値を探索するのではなく、「最適な構造をつくるプログラム自体」を進化させることで、人間が思いつかなかった並べ替えのルールを見つけ出したという。そのルールに従うと、nが2、4、8、16と増えるにつれて、超立方体の次元は「n log n」の規模で、これまでの常識よりも遥かに速く、巨大に成長することが証明されたとしている。

さらに興味深いのは、AIが見つけ出したこの巨大な構造をつくるための並べ替え方が、全く別の分野ですでに使われていたものと一致した、とされていることだ。それは、金融工学における株価変動のシミュレーションや、数値計算のモンテカルロ積分などで用いられる「準乱数」の生成式と本質的に同じものであったという。

Source and Image Credits: Ellenberg, J., Libedinsky, N., Plaza, D., Simental, J., & Williamson, G. (2026). Bruhat intervals that are large hypercubes.