トランプを“適当に”混ぜてちゃんとランダムになるのは何回目？ 必要なシャッフル回数分かる公式を発見か【研究紹介】

米ハーバード大学などに所属する研究者らが発表したプレプリント論文「Universality of Cutoff for Riffle Shuffling」は、カードゲームで誰がシャッフルしても、どんな分け方をしても、混ざるまでの回数を予測できる公式を解明したとする研究報告である。

52枚のトランプをシャッフルする時、何回混ぜれば本当にランダムになるのだろうか。

リフルシャッフルは、カードの束を2つに分けて、パラパラと交互に落としながら一つに合わせる技法である。1992年に、カードを二項分布のもとで2つの山に分けた場合について「7回シャッフルすると急激にランダムに混ざりだす」との結果を含む有名な理論が証明されている。

しかし現実のカードゲームでは、人によって切り方は様々である。きっちり26枚ずつに分ける人もいれば、適当な位置で切る人もいる。この現実的な問題に対して、2000年に半分以外の比率で切る場合にも対応できる理論が登場しているが、切り方が二項分布に従うという制約があった。

今回の研究は、これら先行研究を包含する普遍的な理論を完成させたといえる。論文によると、リフルシャッフルにおいて、どんな分け方をしても、必要なシャッフル回数を正確に計算できる公式を発見したのである。

発見した公式は、N枚のカードに対して必要なシャッフル回数が「Cμ × log N」という形で表されるというもの。ここでμは切り方の確率分布を表し、Cμはその分布によって決まる定数である。

この公式を当てはめると、例えば、ランダムな位置で切る場合（一様分布）では、52枚のトランプに対して約14.25回のシャッフルが必要となることが計算された。また、どのような切り方をしても、デッキを必ず均等に分割する方法より速く混ざらないこともわかった。

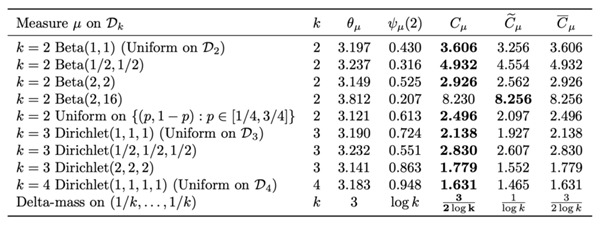
さらに、異なる切り方を交互に行うと、それぞれを単独で行うより効率が悪くなる場合があることが示された。例えば、半分切りと3分の1切りを交互に行うより、どちらか一方を続けた方が速く混ざる可能性がある。これは「複数人で協力すれば効率が上がる」という直感に反する結果である。

今回発見した公式は「コールドスポット」と呼ばれる現象が肝になっている。コールドスポットとは、シャッフルが不十分なときに、デッキの特定の部分で隣り合うカードが元の順番を保っている確率が高い領域のことを指す。研究チームは、この場所を数学的に特定することで、シャッフルが不十分かどうかを見抜き、必要なシャッフル回数の下限を特定している。

Source and Image Credits: Sellke, M., Shi, J., & Wang, J. (2025). Universality of Cutoff for Riffle Shuffling.