ほぼ全ての“回転”を元に戻せる新原理を発見。回転角を調整し2回繰り返すだけ、数学的に解明【研究紹介】

スイスのジュネーブ大学と韓国の蔚山科学技術院（UNIST）に所属する研究者らが発表した論文「Walks in Rotation Spaces Return Home when Doubled and Scaled」は、物体の運動においてどんなに複雑な回転が連続しても、ほぼ確実に元の状態に戻せる原理を数学的に証明した研究報告である。

• keyboard_arrow_down 一つひとつの動きを「逆向きに実行」しなくても
• keyboard_arrow_down 「ちょうど合計180度回転になる速さ」を探す

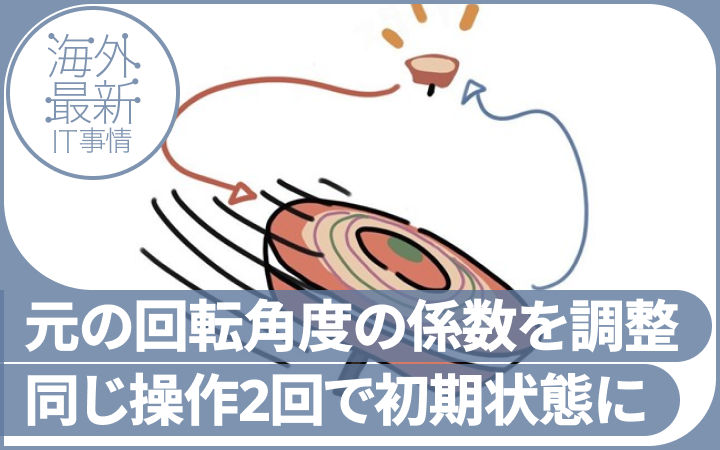
例えばコマを回転させ続けると、最初の状態からどんどんずれていく。通常、元に戻すのは至難の業だ。従来は、複雑な回転の連続を元に戻すには、一つひとつの動きを正確に、逆向きに実行するしかないと考えられていた。

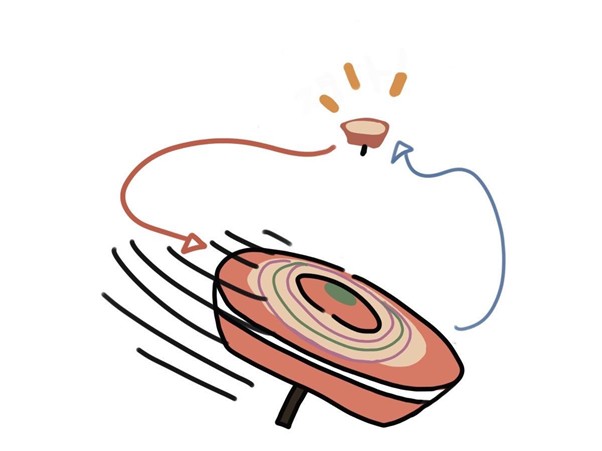
しかし今回の証明により、元の回転角度の係数を適切にスケーリング（速度の倍率調整）し、その操作を2回繰り返すだけで、ほぼすべての場合において初期状態に戻すことができると明らかになった。

この現象を理解する鍵は、3次元空間における回転の性質にある。3次元空間のあらゆる回転を集めた集合を、「SO(3)」という。SO(3)の回転は、回転軸（どの方向を軸に回すか）と回転角度（その軸の周りに何度回すか）で決まる。

これを視覚化するには、回転軸の方向に、回転角度の大きさだけ伸ばしたベクトルを考える。すると、すべての回転は半径180度の球の中の点として表現できる。なぜ180度になるのかというと、270度回転は逆向き軸周りの90度回転と同じ結果になるためである。

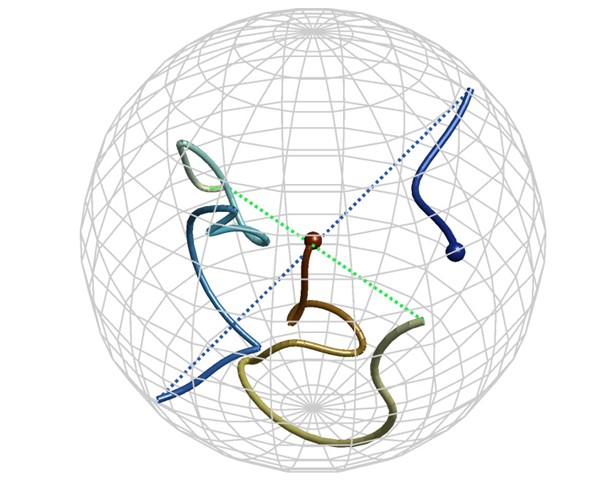
球の中心は回る前の中心点（回転なし、物体が元の状態のまま、恒等回転）と考える。連続的な回転は、そこをスタート地点として虫がリンゴの中をトンネルのように掘り進むように、球内をある点から別の点へと移動する軌跡として表現される。つまり、回転を元に戻すという目標は、球の中心に戻る経路を見つけることである。

しかしランダムに回転を選ぶと、球の中心付近には点が少なくなる現象が起き、中心に戻るという目標を難しくする。例えば、ダーツを適当に投げると、真ん中をほとんど避け、周囲の大きな領域に刺さるのと似た感じである。だから、複雑な回転を何度も繰り返したあとは、球の中心に正確に戻るのは難しいというわけだ。

ところが、同じ回転を2回繰り返すと、2回繰り返した回転の角度分布は完全に一様になり、0度から180度まですべての角度が同じ確率で現れるようになる。これがこの発見の核心である。

分かりやすく説明すると、まずランダムな回転では、130度や160度といった大きな角度が現れる確率が高くなる。しかし160度の回転を2回繰り返すと、合計は320度となり、実質的には360-320=40度の小さな回転と同じになる。つまり、同じ回転を2回繰り返すことで0度から180度まで、どの角度も均等な確率で現れるようになる。

この研究では、これを利用した巧妙な方法を用いる。複雑な回転の連続に対し、すべての回転の速さを同じ割合（倍率を0.7倍にしたり、1.2倍にしたり）で調整する。速くしたり遅くしたりしながら、回転の連続を合計するとちょうど180度回転になる速さを探す。180度回転なら、球の表面全体が的になるので当てやすい。そして180度回転を2回繰り返せば360度、つまり元に戻る。

実際の応用では、磁場の強さがこの「倍率」に相当する。複雑な磁場パルスを受けた電子スピンも、磁場の強さを一様に調整すれば、ちょうど180度回転する強さが必ず見つかる。その磁場を2回かければ、スピンは元の状態に戻る。

この原理は、電子スピン、量子ビット、ジャイロスコープ、原子核、ロボットアームなど、回転するほぼすべての物体に共通する。物体が空間内で非常に入り組んだ経路を通る場合でも、すべての回転角度を同じ係数でスケーリングし、その複雑な軌道を2回繰り返すだけで、原点に戻すことができる。

Source and Image Credits: Eckmann, Jean-Pierre and Tlusty, Tsvi. Walks in Rotation Spaces Return Home when Doubled and Scaled. Phys. Rev. Lett. 135, 147201 – Published 1 October, 2025 https://doi.org/10.1103/xk8y-hycn