「最短経路問題」の新アルゴリズム。数十年来の“理論的限界”破ったと発表【研究紹介】

中国の清華大学、米国のスタンフォード大学、ドイツのMax Planck Instituteに所属する研究者らが発表した論文「Breaking the Sorting Barrier for Directed Single-Source Shortest Paths」は、グラフ理論の最短経路問題において、長年の理論的限界を打ち破るアルゴリズムを発見したとする研究報告である。

グラフ理論における単一始点最短経路問題（Single Source Shortest Path Problem）は、ある地点から他のすべての地点への最短ルートを見つける問題で、カーナビのルート検索やネットワーク設計など、幅広い応用を持つ。

コンピュータサイエンスの基礎的な問題のひとつであり、この問題を解く最も有名な方法が、1959年に考案されたダイクストラ法である。ダイクストラ法は、出発点から波紋が広がるように、近い地点から順番に最短距離を確定していく手法である。この方法は長年にわたって最良とされ、教科書にも載っている標準的な手法となっている。

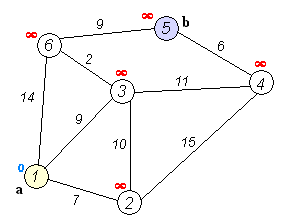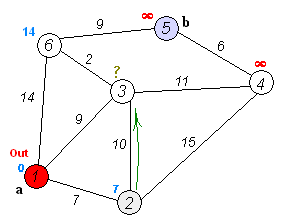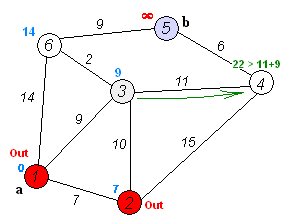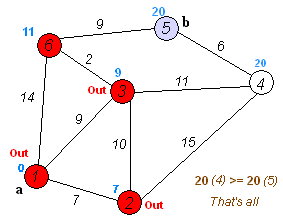
しかし、ダイクストラ法にはひとつの限界があった。それは、すべての地点を距離順に並べ替える必要があることである。地点が多くなると、この並べ替えに時間がかかってしまう。この「ソーティングバリア」（Sorting Barrier）は、長年研究者たちを悩ませてきた理論的障壁だった。

今回研究チームが、この壁を破る新しいアルゴリズムを発表した。新手法は計算時間をO(m log^(2/3) n)に短縮し、辺の数が少ない疎なグラフにおいて、従来の計算時間O(m + n log n)を上回る性能を実現した。これは、ダイクストラ法が必ずしも最適解ではないことを示した点で、学術的に大きな意義を持つ。

新アルゴリズムの鍵となるアイデアは、すべての地点を厳密に距離順に処理する必要はないことにある。研究チームは、処理すべき地点を適切に選別することで、並べ替えの手間を大幅に削減できることを示した。具体的には、「ピボット」と呼ばれる重要な地点だけを選び出し、それらを中心に効率的に探索を進める。

技術的には、従来のダイクストラ法と、別の古典的手法であるベルマン・フォード法を組み合わせている。新手法はこれらの長所を組み合わせ、状況に応じて使い分けることで効率化を実現したことが示されている。

Source and Image Credits: Duan, Ran, et al. “Breaking the Sorting Barrier for Directed Single-Source Shortest Paths.” Proceedings of the 57th Annual ACM Symposium on Theory of Computing. 2025.