「本当の乱数」実現か？　量子コンピュータで予測困難な乱数生成に成功、JPモルガンなど発表【研究紹介】

米JPモルガン・チェース、アルゴンヌ国立研究所、Quantinuumなどに所属する研究者らが発表した論文「Certified randomness using a trapped-ion quantum processor」は、量子コンピュータを用いて、予測困難であることが保証された乱数をつくり出すのに成功したとする研究報告である。

古典的なコンピュータでは真のランダム性を生み出すことは原理的に不可能とされる中、今回の研究チームは56個の量子ビットを持つイオントラップ型量子コンピュータ（QuantinuumのH2-1）をインターネット経由で操作し、古典計算による偽装ではないことを認証できる、7万1,313ビットのランダムビットを生成した。

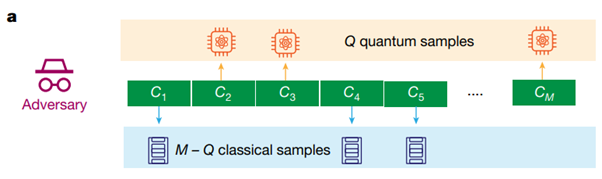
量子コンピュータを使って生成された乱数かを検証する方法としては、既存の古典的なコンピュータでは、量子コンピュータと同じ速さでの計算ができないという点を利用する。つまり、量子コンピュータよりも速く良い品質の結果（乱数）が返せなければ、その乱数は誰かが古典的なコンピュータで計算して偽装したものではないと示せる、というものだ。

実験では、まずテスト側（クライアント）が特殊な計算パターン（量子回路）をつくり、それを量子コンピュータ側（サーバ）に送る。サーバはその計算を実行して結果（各回路に対するビット文字列）を返す。この結果は量子力学の性質により本質的にランダムな内容になる。

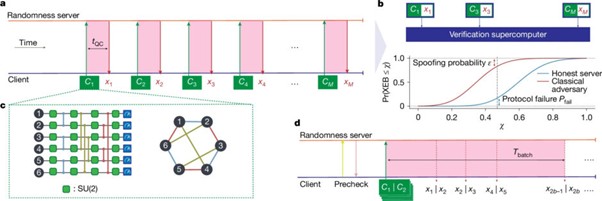
そして、この結果の平均応答時間と「XEB」（Cross-Entropy Benchmarking）スコアと呼ばれる品質指標の両方を用いた検証を行う。平均応答時間が2.2秒以下、XEBスコアが0.3以上という条件を満たせば、サーバが量子コンピュータを使用していると判断できる。普通のコンピュータでは、同じ品質の結果をその速さで出すことは不可能だからだ。

実験では、合計6万952の回路が送信され、3万と10の有効な結果サンプルが得られた。これらサンプルそれぞれが56ビットの長さを持ち、乱数となる。これらの結果は平均2.154秒で返ってきた。これは設定した制限時間（2.2秒）より短い。またXEBスコアも0.32と設定した基準（0.3）より高かった。

検証には世界最高レベルのスーパーコンピュータ複数台（Frontier、Summit 、Perlmutter、Polaris）が使われ、合計で毎秒1.1エクサ回（1エクサは100京）の演算を行った。この膨大な計算力を使っても、量子コンピュータほど速く高品質な結果は出せないことが確認された。

最終的に、研究チームは量子コンピュータを使って、条件下で7万1,273ビットの予測困難な乱数をつくり出した。これは、世界最速のスーパーコンピュータの4倍の能力を持つ計算機を使っても再現できないレベルである。つまり、その値を事前に予測したり操作したりすることができない「公平な乱数」ということになる。

このランダム生成技術は、情報セキュリティ分野での応用が期待される。また複数の人がその場でつくられた公平さを必要とする場面で応用できる。例えば、オンライン宝くじや電子ゲームなどで、誰も操作できない公平な乱数は有用である。

Source and Image Credits: Liu, M., Shaydulin, R., Niroula, P. et al. Certified randomness using a trapped-ion quantum processor. Nature (2025). https://doi.org/10.1038/s41586-025-08737-1