【スゴ本】思わず数学を学び直したくなる5冊

• keyboard_arrow_down はじめに
• keyboard_arrow_down 天才が数学で「あそぶ」方法を学ぶ
• keyboard_arrow_down 数学好きの高校生がゲーデルの不完全性定理に取り組む
• keyboard_arrow_down 3週間で高校数学をやり直す
• keyboard_arrow_down 美しさを追求する
• keyboard_arrow_down 生物学への応用
• keyboard_arrow_down おわりに

職業人100人に「あなたが仕事で使う数学は何ですか？」と聞いた結果がこれ。

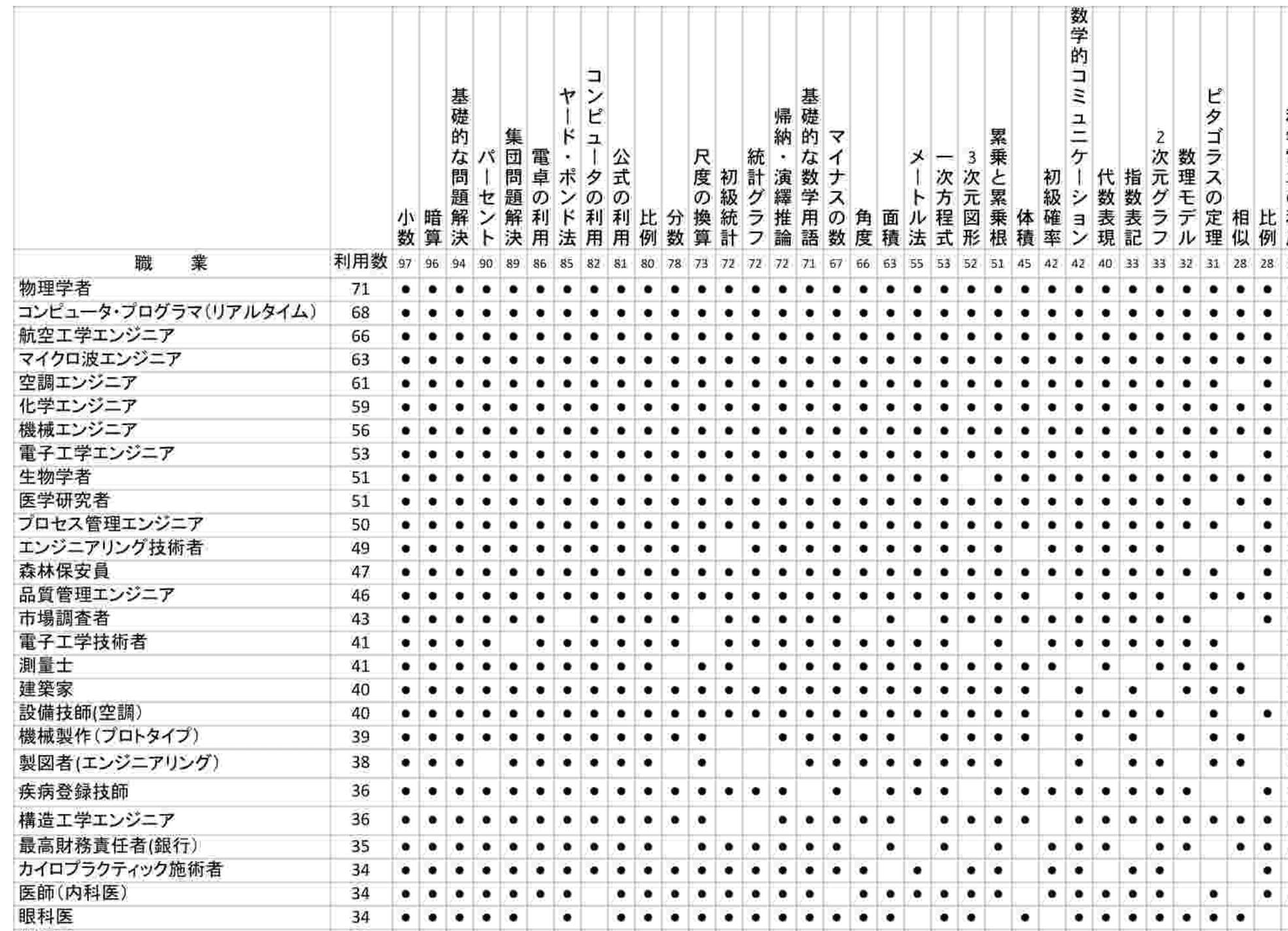
横軸には、微積分とか因数分解といった数学の単元が並んでおり、縦軸には、数学を使う順に職業がランキングされている。Hal Saunders氏の『When Are We Ever Gonna Have to Use This?』を元に、作家で読書家の読書猿さんがまとめたものだ。

これによると、ITエンジニアは、数学を使う職業の第2位になる（ちなみに1位は物理学者）。

もちろん、プログラミングするとき、数学的な理論を直接駆使しているわけではない。UIのデザインやAPI開発は、一見すると、数学から離れたものに見える。

だが、数学を単なる計算ツールとして捉えるのではなく、問題解決のための論理的思考として考えるならば、数学を使う職業第2位というのも納得がいく。

例えば、複雑な問題に取り組むとき、問題を適切な大きさに分解して、前提を明確にした上で、利用できるパターンに当てはめ、体系的に解く。これはプログラミングにおける設計作業だといえる。

あるいは、想定した結果が得られないとき、どこで問題が起きているか段階的に切り分けてエラーを特定する。応用問題や証明でさんざんやってきたプロセスだが、ITエンジニアにとってはデバッギングそのものになる。

日々のプログラミングにおいて、数学の公式や定理を直接使う機会は少ないかもしれないが、数学的に考えるフレームワークは空気のように自然なものだろう。

ここでは、そんなITエンジニアに向けて、もともと持っている数学的思考をさらに深めたり、楽しく学び直し、数学的なセンスを磨いたりするのに役立つ本を紹介する。

1冊目は、『数字であそぼ。』のご紹介。数学の面白さと恐ろしさの両方を、爆笑しながらいっぺんに学べる。

主人公は頭を抱えている横辺くん。天賦の才能を持っており、一度読んだだけで中身を完璧に覚えることができる。フォトグラフィックメモリーという能力で、写真記憶や映像記憶というやつだ。

教科書や参考書を完璧に覚えていられるから、テストはいつも100点満点で、天才とも神童とも呼ばれ、西の雄である吉田大学（絵面はどう見ても京都大学）に一発合格する。

そんな彼がなぜ頭を抱えているのか？

それは数学が壊滅的にできないから。大学入試までの数学は、定理や公式を覚えて問題に当てはめれば正解を導ける。

ところが、大学の数学の一発目の授業で挫折する。先生は「数をつくりますねー」と言いながら有理数や自然数の定義を並べる。「数をつくる」ってどういうこと!? 混乱をヨソに、先生はどんどん話を進めていく（内容からするに、デデキント切断※の概念らしい）。

※ デデキント切断…実数を有理数の集合の分割によって定義する方法。 全ての有理数を2つの集合に分け、どちらにも最大値がない、あるいは片方にのみ最大値が存在するように分割することで、無理数も含めた実数を表現する。

もちろん黒板に書いてあることは一目で覚えられる。けれどもそれが何を意味しているのか理解することができない。「分かる」というのがどういうことなのか分からなくなり、真っ白に灰化してしまう―――で、絶望して学校に行けなくなって2年の月日が経過するところから、物語はスタートする。

単位ゼロ、いきなり2留というのもシビアだが、「数学が分かりたい」という動機で、よりによって数学科を選んでしまう。親切にしてくれた同級生や教授が、みんな数学科だったという縁もあるが、この連中が曲者なのだ。

数学的センスは抜群なのに生活力ゼロで汚部屋に住んでる美女子、優秀なのにパチスロ沼にハマり、ギャンブルを数学で解こうとする奴、お風呂で数学してるうちにそのまま徘徊して職質される教授など、「数学やってる人は変人」という世間の偏ったイメージそのままのキャラクターだ。

奇人変人だらけのキャンパスライフというと、獣医学部の奇妙な面々を描いた『動物のお医者さん』を思い出す人もいるかもしれない。その数学科版といっていいかも。

随所に数学ネタが織り込まれており、「数学の専門家にとって1+1=は難しい」とか「ホールケーキを7等分する方法」「マッチングアプリで何人目と付き合うのが最適か？」といったお話が楽しい。タイトルどおり「数字」で遊ぶパズルみたいに楽しめる。

一方で、「銭湯のタイルを使ってカントールの対角線論法をする」や「ルベーグ測度を使って、こけしを畳一面に埋め尽くす」「バナッハ・タルスキーの定理で幽霊を考える」といった話では、ネタの向こうに数学の世界の深みをチラリと垣間見ることができる。

最初は「数字」で遊んでいるうちに、だんだん「数学」で遊ぶようになってくる。

2冊目は女子高生が数学を手ほどきする『数学ガール』。

数学をテーマにした小説で、数学と仲良くなれるシリーズものだ。主人公の「僕」と、数学に情熱を持つ個性豊かな3人の少女たち（ミルカさん、テトラちゃん、ユーリ）とのやり取りが楽しく、甘酸っぱさを掻き立てる。

中学・高校生からでも読んでもらえるように、「なぜそうなるのか？」「どうしてそう言えるのか？」といったプロセスに重きを置いており、文字通り、ステップバイステップで解説してくれる。

さらに、物語形式のため、数学に苦手意識がある人でも親しみやすく、「数学にもう一度向き合いたい」という人にもお薦め。シリーズものだけど、各巻で異なるテーマで構成されており、どこから読んでもいいし、気になる巻だけ読んでもいい。

ここでお薦めするのは、ゲーデルの不完全性定理の巻だ。

中二病を拗らせて「数学という人類最大の論理体系さえも不完全だ」と語りたい人が持ち出すのがゲーデルのこの定理だが、本書を読むとぜんぜん違うことが分かる。

最初は、論理パズルや小話的なトピックが並んでおり、「ウソつきのパラドクス」や「0.999…は1に等しいか」「数学的帰納法」でウォーミングアップする。「僕」と女の子たちの掛け合いを楽しみながら、基礎を固めていく仕掛けになっている。

そして、そこで学んだことを用いて「ペアノの公理」「イプシロン・デルタ論法」「公理と定理」「数学における証明とは何か」「無限」といったテーマを深掘りしていく。数学がどのように成り立っているかを考察したり、数学の論理構造を厳密に考えるシミュレーションができる。

最後には、大テーマとなる「ゲーデルの不完全性定理」に挑む。これまで学んできた知識を総動員して、「完全な数学の公理体系は存在しない」という結論を導く。ここは黒髪銀縁眼鏡のミルカさんの独壇場で、論理的な飛躍を一切せず、省略抜き、ガチンコに証明する。

本書が素晴らしいのは、一冊で完結していることだ。「ゲーデルの不完全性定理とは何か？」という問題に答えるために必要な数学的手法・アイデア・公理体系は、全て序盤〜中盤で準備されている。比喩や例の置き換えも事前に説明されており、一歩一歩進んでいけば、必ず到達できるように構成されている。

不完全性定理を紐解いていくと、数論や論理学の形式体系、集合論や無限の扱いなど、様々な知識体系が必要となる。それら全部を学びなおすのは大変すぎる。だが、本書を用いることで、不完全性定理を理解するために必要な、ちょうど良い範囲で各理論を学ぶことができる。

もちろんここで触れた理論でさらに知りたければ深掘りすればいい（そのための読書案内や参考文献も示してくれる）。数学が繋がっていることを実感するはずだ。

3冊目は、3週間で高校数学でやり直すための『新体系・高校数学の教科書』だ。

本書の特徴は、「つながり」だ。アラカルト方式を改め、高校数学の体系を一本化しているという。

上巻の「数と式」の和と差の積の形に半ば強引に持ち込むテクは、下巻の積分の展開でガンガン使うし、図形と関数はベクトルと行列の基礎訓練だったことに気づかされる。ベクトルが行列に、行列が確率行列に、さらに行列がθの回転運動や相似変換に「つながっている」ことが分かったとき、目の前がばばっと広がり、強制覚醒させられる。

「教科書」とタイトルにあるが、単なる教科書的な解説に留まらない。生活やビジネスの現場と数学の世界とのつながりを重視し、数学のモデルの説明に力点を置いているところが良い。

例えば、整式と分数式の章では、ドント方式（比例代表制度における得票の分配方式）の事例を出してくる。単純にドント式の説明だけではなく、「もし政党が合併したら得票数はどうなる？」といった生々しいシミュレーションを解説する。

あるいは、一次不等式の説明の際、ビジネスの現場では線形計画問題として応用されると説く。限られた予算や条件下で最大のアウトプットを出す計画を立案する際に使える方法論だ。もちろん机上の計算通りになるかどうかは分からないが、計算式として可視化しない限り、稟議は通らない。

著者の主張は、高校数学で学べる数学のモデルを通して、ストラテジー（発見的問題解決法）を身につけろというものだ。これは、個々の具体的な問題に対するテクニックとは異なるものだ。何らかの発想上の工夫を見つけないと解けない問題を解決するための手段を、いくつかの型に一般化しなさいというのだ。

この考え方は、昔ならチャート式、今ならデザインパターンになる。例えば、「～が分かるためには、……が分かればよい」という推論をいくつかくり返す「逆向きにたどる」方法や、問題を特殊な状況に落とし込むことによって解決しようとする「特殊化」、既知の解決法を新たな問題にあてはめようとする「類推」といった手法が、演習で解説される。クルマの運転やビジネスプロセスと一緒で、実際に動かして身につける能力だろう。

やり方を覚えて答えだけ導けばよい、という受験対策ではなく、自分で組み立てられることが大切だと説く。かつて暗記数学でしのいだ私の耳に痛い。

高校のときと明らかに違うのは、テストするのは、自分であること、期限がないこと。期末試験も受験もない。好きなだけしがみついてもいいし、早々とあきらめてもいい。基礎に立ち戻るには、教科書を勧めたい。

4冊目は「見る数学」である『美しい幾何学』を推したい。

ただ眺めているだけで、その美しさが伝わってくる。

教科書ならモノクロで印刷される定理や図形を、鮮やかなモダンアートにして魅せてくれる。オイラー線やサイクロイド、シュタイナーの円鎖など、単体でも美しいフォルムをカラフルにリデザインしており、ページを繰るだけで楽しくなる。ひまわりやオウムガイの螺旋に見られる、形のなす必然に心が奪われるだろう（たとえフィボナッチ数の話を知っていたとしても）。

同時にこれは、「知る数学」でもある。直感だけで受け取った美には、そのパターンを支えるシンプルな定理が存在し、かつそれは、なるべくしてそうなっていることに気づかされる。この必然性を知るためには、やはり定理を解き、式を理解する必要がでてくる。編集方針なのだろう、数式を控えめに、なるべく「見て分かる」ようにしている。この、簡潔だけど丁寧に解説する知的態度を伝えるのが難しい。

さらに、中学で習った三平方の定理のすぐ脇に、奥深い無限の世界が口を開けていることも、見える化されている。もちろん無限は描き尽くせない。だが、どっちへ進むとそうなるかは、描ける。有理数とイコールで結ばれた（完結した）世界から、いきなり果てのない深淵の扉が開くのは、実は怖いことなんだと、あらためて教えられる。アルキメデス学派がタブー扱いするのも分かる。量を測るための数学が、量をなくしてしまうことになるから。頭で分かってはいても、見えるようにするとゾッとなる。

たとえば、表紙のシェルピンスキーの三角形はこんなプロセスで出来上がる、フラクタルな無限である。

1. 1. 正三角形を描く
2. 2. 正三角形の各辺の中点を結んだ正三角形を描く
3. 3. 中央の正三角形を取り除く
4. 4. 上記2.と3.を繰り返す

最初の三角形の面積を1とすると、次の3つの三角形のそれぞれでは、面積が1/4で、全部を合わせた面積は、3*(1/4)=3/4になる。次のステップで9個の黒い三角形の面積は1/16で、総面積は9*(1/16)=(3/4)^2となる。これを続けていくと、残った部分の面積は、数列1,3/4,(3/4)^2,(3/4)^3…となり、公比3/4の等比数列となる。

公比は1未満のため、数列の項は、n→∞のときに0に限りなく近づく。そのため、最終的には元の三角形は、各段階で黒い領域の1/4だけを取り除いたにもかかわらず、消えてしまうことになる。表紙のシェルピンスキーの三角形は、わずか6ステップしか踏んでいないのに、既に完璧な「篩」（ふるい）になっている。面積という、見える有限の「量」が無限のステップの中で消えてしまう不思議。

その一方で、三角形の周長は、一辺1とすると、3,9/2,27/4,81/8…となる。これは公比3/2の等比数列で、公比は1より大きいので、より多くの三角形を取り除くにつれて、項は際限なく大きくなり、周長は無限に大きくなってゆく……面積がゼロに限りなく近づく一方、無限の長さをもっている！

ありふれた三角形から、この世のものではない無限を導き出し、それを見せてくれる。プロセスとして無限の扱い方は知ってはいるが、実感となると慄くだろう。

そういう、数学の美しさと恐ろしさを魅せてくれる一冊だ。

5冊目は『数学で生命の謎を解く』のご紹介。

著者は、「20世紀における数学の推進力が物理学だとしたら、21世紀のそれは生物学となるのではないか」という問題意識を持っており、生命を数学で説明する試みが本書になる。

最初は入りやすいエピソードから始まる。コッホの顕微鏡やメンデルの遺伝から始まり、ダーウィン、DNAをおさらいした後、観察倍率を拡大し、時間を早送りする。分子レベルのDNAの振る舞いや、ヒトゲノム計画、ウイルスの構造、細胞の構成、ウイルスの形や行動、および生態系の相互作用まで深堀りする。

この構造は、生物学の歴史をトレースするようだ。

生物学とは、始めの頃は植物や動物に関する学問だった。次に細胞に関する学問となり、現在では、複雑な分子に関する学問となっている。生物学の観察対象の変化に合わせ、本書では、日常の人間のレベルからはじめ、生物の微細な構造にどんどん細かく焦点を合わせていき、最終的に「生命の分子」であるDNAにたどりつく。

本書のキモは、それぞれの詳細化の過程で、応用数学を適用する事例を紹介する点にある。生物学のフロントラインだけでもじゅうぶん刺激的なのに、そこに数学の応用を見出すことはスリリングな読書になる。

葉序（ようじょ）における黄金比の役割や、フィボナッチ数、ダイナミクス、カオス理論、対称性、ネットワーク、力学、弾性理論、結び目理論と多岐にわたる。そこで紹介される研究成果が興味深い。

例えば、粘菌を使ったネットワークが、関東平野の鉄道網に酷似している事例が紹介される（[粘菌の輸送ネットワークから都市構造の設計理論を構築]）。主要都市を粘菌の餌として、餌の場所どうしをつなぐネットワークを粘菌がどのように作っていくかの実験だ。コンピュータでシミュレートした「最善の」アルゴリズムを、粘菌がどうやって見つけているかが分からない。試行錯誤？　でも粘菌って全体が「見えて」いるの？　ネットワーク障害に対する頑強性や脆弱性について理解が深いと、腑に落ちるのかもしれない。

一方で、私の「常識」をひっくり返す主張もある。

オウムガイやヤギの角の形状に見出せる「黄金比」は、数学的な都市伝説だという主張だ。角や殻の形は、一周ごとに一定の割合（成長率）で拡大する、対数らせんに近い。

確かに成長率が黄金比と関連するような対数らせんは存在するが、それは測定データの中から都合の良い箇所を抜き出したり、たとえ統計的に異なる成長率が存在しても、ある条件で黄金比が「見つかった」と結論付けたりしているというのだ。

統計分析の手法を使って、データを黄金比の周りに集中させる、一種の数秘術なんだって。このやり方で名画や建築物に強引に黄金比を当てはめることもできる。着眼点をいじれば、黄金比はいくらでも出てくるのだから。

本書での新しい斬り口は、知性（intelligence）の扱いについてだ。進化と知性のありかたについて、非常に興味深い視点を与えてくれる。

知性（intelligence）は、哺乳類でも進化したため、普遍的特徴である。しかし、extelligenceと呼べる、文化的智識やノウハウを、自分の身体の外に、誰もが手にできるような形で蓄積する能力は、地球上では一度しか進化していないという。

例えば言語や文字、図像、インターネットのようなものがその典型的な例だ。これは、宇宙レベルで見た場合でも、人類に特有のものであり、一度きりの偶然の産物になるのだろうか？

著者はそう考えていない。単なる偶然ではなく、進化の過程で強力な適応戦略として機能する普遍的な仕掛けだと主張している。

つまり、異なる進化の環境でも、extelligence的な仕組みは何らかの形で生じる可能性が高いというのだ。別の場所で進化をやりなおすなら、「ことば」に相当する／成り代わるものが何になるのか、想像するだけで面白い。

それは、特定の視覚的信号（色やパターン、形）だったり、触覚や振動、あるいは匂いや化学的な信号を用いた伝達情報であったとしても、extelligenceを構築する上での可能性として考えられる。

私たちが紙にエンピツで書くように、気体の組成の組み合わせで記録されているextelligenceがあるかもしれないと考えると胸アツになる。

以上、数学をやり直し、数学的なセンスを磨く上で役立つ書籍を紹介した。

最初はウォーミングアップとして、数学で遊ぶための『数字であそぼ。』だ。数学にハマった吉大生（ホントは京大生）たちの奇人変人っぷりを笑っているうちに、それだけ深いところを考え抜いているんだ……と、ヒヤッとする世界を垣間見ることができる。

次は、ゲーデルの不完全性定理を完全攻略する『数学ガール』を紹介した。まとめサイトやまとめ動画にある「例え話」ではなく、一歩一歩自分で理解するためのプロセスを経たうえで理解することができる。それぞれの理論や手法や数学モデルは前半で説明してくれるので、文字通り一冊で理解（わか）ることができる。

3冊目は、数学をやり直す基本となる『新体系・高校数学の教科書』を紹介した。手を動かし、数学的思考を反復練習するにはうってつけといえる。短期間でイッキにやることをお薦めする。そうすることで、各単元の繋がりがより見えてくるはず。

4冊目は、数学の美しさと恐ろしさを視覚化した『美しい幾何学』のご紹介。数式の概念を幾何に落とし込むことで、そのパターンを形状化させる。それと同時に、なぜその形状なのかを理屈として説明するお得な一冊だ。

5冊目は、生命の営みを数学で説明した『数学で生命の謎を解く』だ。数学を用いることで、生命の進化や人類以外の知性の存在を説明できるか？という疑問に挑戦した、野心的な一冊でもある。著者と応答しながら、「自分ならこう考える」とツッコミを入れながら読むと楽しい。

楽しく数学を学び直し、あなたが持っている数学的なセンスや思考様式を磨く上で役に立つと嬉しい。逆に、「それが良いならこれなんてどう？」とお薦めしてくれると私が嬉しい。